编程语言php

Exploring the World of ILP Programming Language

Introduction to ILP:

ILP stands for *Integer Linear Programming*, a mathematical optimization technique used to find the best solution to a problem involving a linear objective function and linear inequality or equality constraints. While ILP itself is not a programming language in the traditional sense, it forms the basis for various programming languages and libraries that implement ILP solvers.

Key Concepts of ILP:

1.

Objective Function:

In ILP, the objective function is a linear equation that needs to be maximized or minimized.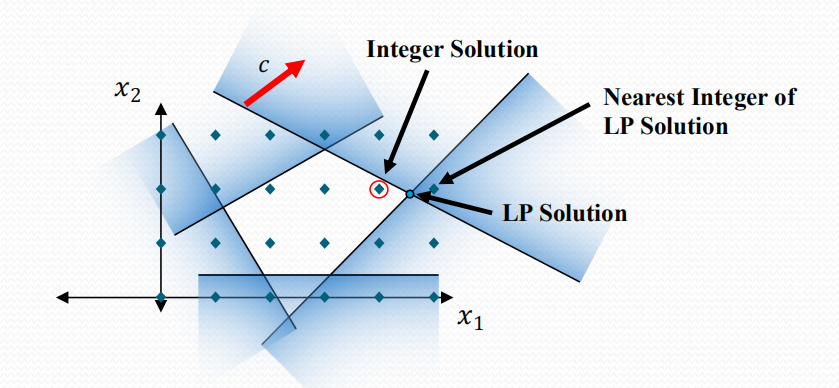

2.

Constraints:

These are linear inequalities or equations that restrict the values of the decision variables.

3.

Decision Variables:

These are the variables whose values need to be determined in order to optimize the objective function.

4.

Integer Solutions:

Unlike linear programming (LP), ILP restricts the decision variables to integer values, adding complexity to the optimization process.

5.

ILP Solver:

A software tool or library that implements algorithms to find the optimal solution to an ILP problem.

Commonly Used ILP Programming Languages:

1.

AMPL (A Mathematical Programming Language):

AMPL is a highlevel language specifically designed for expressing optimization problems, including ILP. It allows users to formulate optimization models in a natural, algebraic syntax.

2.

Gurobi:

While Gurobi is primarily known for its ILP solver, it also provides APIs in various programming languages like Python, MATLAB, Java, and .NET, allowing users to formulate and solve ILP problems programmatically.

3.

PuLP:

PuLP is a Python library for linear optimization that provides a highlevel interface to various LP and ILP solvers. It allows users to define optimization problems in a concise and readable syntax.

Example Code in PuLP (Python):

```python

from pulp import LpMaximize, LpProblem, LpVariable

Create a LP problem

prob = LpProblem("example", LpMaximize)

Define decision variables

x = LpVariable("x", lowBound=0, cat='Integer')

y = LpVariable("y", lowBound=0, cat='Integer')

Define objective function

prob = 3 * x 2 * y

Define constraints

prob = 2 * x y <= 10

prob = x 3 * y <= 12

Solve the problem

prob.solve()

Print the results

print("Optimal Solution:")

print("x =", x.value())

print("y =", y.value())

print("Objective =", prob.objective.value())

```

Guidelines for Using ILP:

1.

Formulate the Problem Correctly:

Clearly define the objective function and constraints of the optimization problem before attempting to solve it.

2.

Choose the Right Solver:

Different ILP solvers may perform differently on different types of problems. Experiment with multiple solvers to find the most efficient one for your problem.

3.

Preprocessing:

ILP problems can often benefit from preprocessing techniques such as constraint propagation and variable fixing to reduce the problem size and improve solver performance.

4.

Integer vs. Continuous Variables:

Be mindful of whether your problem truly requires integer solutions. If not, consider formulating it as an LP problem instead.

5.

Sensitivity Analysis:

After obtaining the optimal solution, perform sensitivity analysis to understand how changes in problem parameters affect the solution.

Conclusion:

ILP is a powerful optimization technique widely used in various fields such as operations research, logistics, finance, and engineering. By understanding its principles and leveraging appropriate programming languages and libraries, practitioners can efficiently solve complex optimization problems to achieve desired outcomes.

Tags： 光遇梦想季入口 平安壹钱包 赛尔号布莱克

版权声明： 免责声明：本网站部分内容由用户自行上传，若侵犯了您的权益，请联系我们处理，谢谢！联系QQ：2760375052