vector用法csdn

Title: Understanding the Usage of Vectors in Various Fields

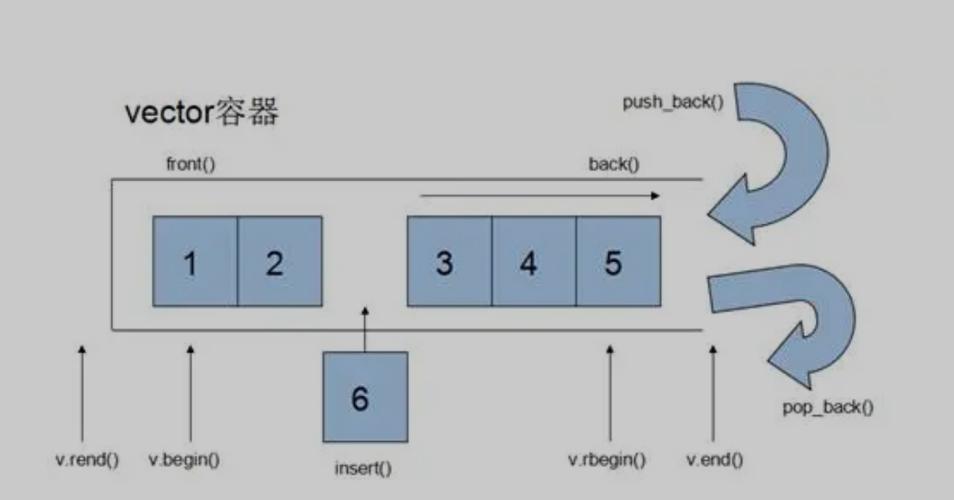
Vectors are fundamental mathematical entities with versatile applications across numerous industries and disciplines, ranging from physics and engineering to computer graphics and data science. Let's delve into their usage and significance across these fields.

1. Physics and Engineering:

In physics and engineering, vectors are indispensable for representing quantities that have both magnitude and direction. They are extensively used in:

Force Analysis

: Vectors help describe forces acting on objects. Each force has a magnitude (strength) and direction, represented by arrows in diagrams. Understanding vector addition is crucial for resolving complex force systems.

Motion Analysis

: Vectors describe the velocity and acceleration of objects. Velocity, for instance, is a vector quantity comprising speed and direction. By employing vectors, physicists and engineers can analyze the trajectory of projectiles, motion of celestial bodies, and dynamics of mechanical systems.

Electric and Magnetic Fields

: Vectors are employed to depict electric and magnetic fields. The direction of the vector at any point indicates the direction a positive charge would move, providing insights into electromagnetic phenomena.

2. Computer Graphics:

Vectors play a pivotal role in computer graphics, facilitating the creation and manipulation of images and shapes. They are utilized in:

Geometric Transformations

: Vectors represent points, lines, and shapes in a coordinate system. Transformations such as translation, rotation, scaling, and skewing are executed through vector operations, enabling the rendering of complex scenes in 2D and 3D graphics.

Bezier Curves and Splines

: Vectors are employed to define smooth curves and surfaces in computeraided design (CAD) and animation software. Bezier curves, characterized by control points and interpolation, are widely used for generating aesthetically pleasing curves and shapes.

Vector Graphics

: Unlike raster graphics, which are pixelbased, vector graphics utilize mathematical equations to describe shapes. This scalability enables vector images to be resized without losing quality, making them suitable for logos, icons, and illustrations.

3. Data Science and Machine Learning:

In the realm of data science and machine learning, vectors serve as the backbone for representing and analyzing data. They find applications in:

Feature Representation

: Vectors are employed to represent features in datasets. Each feature corresponds to a dimension in the vector space, facilitating mathematical operations and analysis. Techniques like word embeddings represent words as highdimensional vectors, capturing semantic relationships.

Clustering and Classification

: Vectors are used to represent data points, enabling algorithms to group similar data points together (clustering) or assign labels to them (classification). Methods like kmeans clustering and support vector machines rely on vector representations for analysis and prediction.

Dimensionality Reduction

: Highdimensional data can be challenging to visualize and analyze. Dimensionality reduction techniques such as principal component analysis (PCA) and tdistributed stochastic neighbor embedding (tSNE) transform highdimensional vectors into lowerdimensional representations while preserving essential characteristics.

Guidance and Recommendations:

Master Vector Operations

: Gain proficiency in vector addition, subtraction, scalar multiplication, dot and cross products, as these operations underpin various applications across disciplines.

Practice Visualization

: Develop skills in visualizing vectors in both geometric and abstract contexts. Tools like graphing software and programming libraries can aid in visualizing vector relationships and transformations.

Explore Applications

: Delve into specific applications of vectors within your field of interest. Understanding how vectors are utilized in realworld contexts can deepen your appreciation for their significance.

By grasping the utility of vectors across physics, engineering, computer graphics, data science, and beyond, you can leverage their power to solve problems and innovate within your respective domain.

For further exploration and practice, consider implementing vectorrelated algorithms and simulations, and engage in interdisciplinary collaborations to witness firsthand the transformative impact of vectors across diverse fields.

Conclusion:

Vectors serve as versatile mathematical entities with applications spanning physics, engineering, computer graphics, data science, and beyond. By comprehending their usage and significance within different domains, individuals can harness the power of vectors to solve complex problems, drive innovation, and advance knowledge across disciplines.

References:

Press, William H. et al. "Numerical Recipes: The Art of Scientific Computing." Cambridge University Press, 2007.

Goodfellow, Ian et al. "Deep Learning." MIT Press, 2016.

Foley, James D. et al. "Computer Graphics: Principles and Practice." AddisonWesley, 1995.

Tags： 抢红包攻略 苏妲己图片 红警单机版 冰火人小游戏 星之卡比镜之迷宫金手指

版权声明： 免责声明：本网站部分内容由用户自行上传，若侵犯了您的权益，请联系我们处理，谢谢！联系QQ：2760375052