您所在的位置:首页 - 科普 - 正文科普
1.DiscreteMathematics
![]() 惜蕾
2024-04-16
【科普】
252人已围观
惜蕾
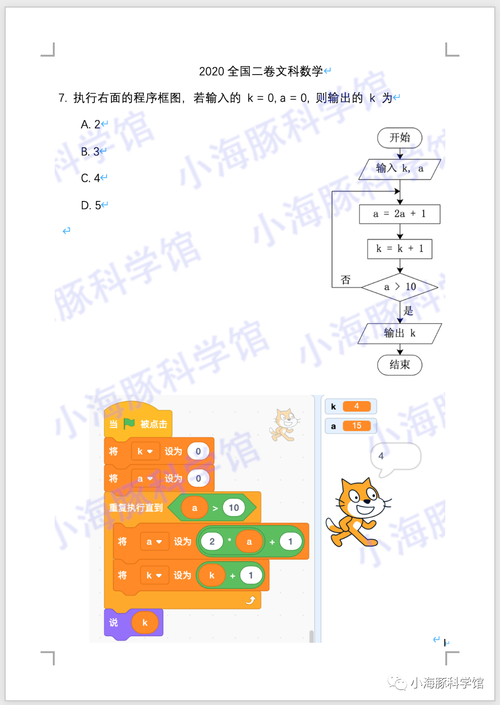
2024-04-16
【科普】
252人已围观
摘要IntermediateProgrammingMathematicsIntermediateProgrammingMathematicsProgrammingandmathematicsareclos
Intermediate Programming Mathematics
Programming and mathematics are closely intertwined, and having a good understanding of mathematical concepts can greatly enhance your programming skills. In this guide, we will explore some intermediate level mathematical topics that are commonly used in programming.
Discrete mathematics plays a crucial role in programming, especially in areas such as algorithms, data structures, and cryptography. Some key topics to focus on include:
- Graph Theory: Understanding graphs, trees, and algorithms like Dijkstra's and Prim's.
- Combinatorics: Permutations, combinations, and probability theory.
- Number Theory: Prime numbers, modular arithmetic, and RSA encryption.
Linear algebra is essential for tasks like image processing, machine learning, and computer graphics. Some important concepts to study are:
- Matrix Operations: Addition, multiplication, inversion, and determinants.
- Eigenvalues and Eigenvectors: Used in principal component analysis and solving differential equations.
- Vector Spaces: Understanding subspaces, basis, and linear transformations.
Probability and statistics are fundamental in areas like machine learning, data analysis, and simulations. Key topics to master include:
- Probability Distributions: Normal, Poisson, Binomial distributions, and their properties.
- Hypothesis Testing: Understanding p-values, confidence intervals, and statistical significance.
- Regression Analysis: Linear regression, logistic regression, and model evaluation techniques.
Calculus is used in optimization problems, physics simulations, and numerical analysis. Some important calculus topics for programming are:
- Differential Calculus: Derivatives, chain rule, and optimization using derivatives.
- Integral Calculus: Definite and indefinite integrals, numerical integration methods.
- Multivariable Calculus: Partial derivatives, gradients, and optimization in multiple dimensions.
Computational geometry deals with algorithms for solving geometric problems. It is essential for tasks like computer-aided design, robotics, and computer graphics. Key concepts to focus on include:
- Convex Hulls: Graham scan, Jarvis march algorithms for finding the convex hull of a set of points.
- Line Intersection: Determining if and where two lines intersect in 2D and 3D space.
- Voronoi Diagrams: Partitioning space based on nearest neighbors and applications in clustering.
By mastering these intermediate mathematical topics, you will be better equipped to tackle complex programming challenges and develop efficient algorithms. Continuous practice and application of these concepts in your programming projects will further solidify your understanding and skills. Remember, mathematics is the language of programming, and a strong foundation in mathematical principles will set you apart as a proficient programmer.